Pae

PAE&FLD: 从大型非结构化运动数据中以无监督方式学习周期性特征。

FLD

• 偈子 法相在皮相之下，真身在假身之中；见所相非相，即见如来

历史研究

使用数据驱动的方法对机器人的运动动力学建模是近年来的热门方向

一种技术路线是使用 RL 方法从仿真中学习策略，该方法在多种机器人上已经表现出较好的效果，但学习速率还是较慢，并且涉及出一个合适的奖励函数是较为困难的

另一种技术路线是模仿学习，学习专家的运动轨迹，学习较好的运动模式，其缺点在于需要高质量的专家数据并且对未曾见过的状态缺乏应对能力

对于基于参考轨迹的运动学习技术，一个关键的问题在于基于轨迹数据学习得到的策略往往只是记住轨迹实例，而不是理解潜在的动力学结构，这导致这些方法的泛化能力较差。同时，高度的非线性与嵌入的高级别相似性阻碍了有效识别与建模运动模式的动力学。

PAE

PAE (period autoencoder) 周期性自编码器，是一种新型神经网络架构。它可以以无监督的方式从大型非结构化的运动数据集中学习周期性特征。

1. 引入

自编码器： 首先，了解一下自编码器(autoencoder)和潜在特征(latent embedding)是什么

• 初期：1980年代，自编码器研究主要集中于如何对神经网络进行数据压缩与降维
• 发展：2000年左右，随着深度学习的发展，自编码器用于无监督学习与数据压缩
• 现状：2010年以来，

autoencoder 主要通过编码器 encoder 将输入数据压缩为低维表示，再通过解码器 decoder 重建原始输入

插值： 插值是一种数学方法，通过已知的数据点估计未知数据点的值，传统的插值方式通过选择合适的插值函数进行插值，以期通过已知的数据点构造一个函数或曲线，进而估计其他未知数据点的值

注意：与拟合不同的地方在于，拟合曲线不一定要经过所有数据点

流形： 流形是一种数学概念，其描述了一种在局部看起来像欧式空间的拓扑空间，n维流形即局部可以近似为一个n维欧式空间(与一个n维欧式空间同胚)。一个典型的例子即地球表面是一个二维流形，在局部区域，可以用二维坐标系(经纬)描述

PAE: 对于 PAE 而言，通过自编码器将动作数据降维分解到多个潜在特征，不同特征捕获身体不同部位随时间变化的非线性周期性。在 latent embedding 的空间中，可以有效的对不同动作进行聚类并通过 decoder 重建比原始运动空间更好的流形

PAE的目标： 学习运动空间的时空结构可以对运动数据插值，在不同类型的运动内部和之间产生真实的过度，生成良好的真实的运动数据

困难： 由于运动数据采集困难导致的稀疏性，运动空间高维非线性的特点，导致传统的简单(线性)插值并不理想，例如最近邻、样条方法以及拉格朗日方法的插值等。

解决方法： 关注运动在时间和空间上的局部周期性，整体动作可以作为多个局部周期性运动的组合。构建一个通用的运动流形结构，参数由相位、频率、偏移和幅度组成

2. 神经网络结构

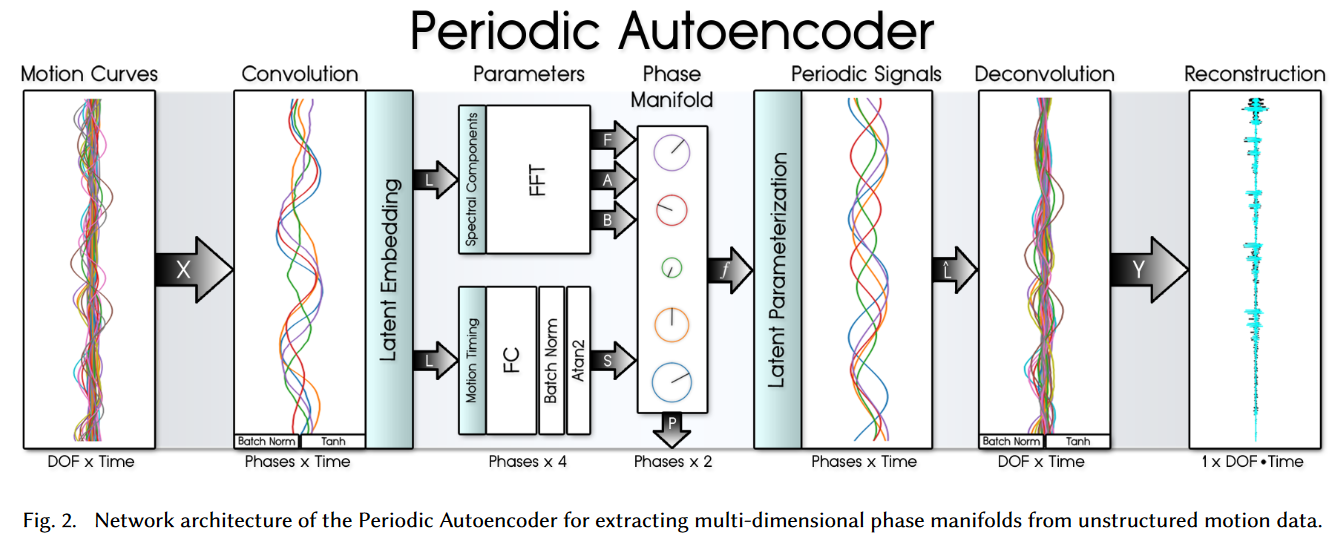
• 输入：不同位点的原始运动曲线 Motion Curves，\(X \in R^{d \times N}\)，d 是身体自由度，例如base_pos dof_vel等，N 是时间帧数；在图中可以看到，很多个曲线混合，每条曲线代表一个维度随时间帧的变化。

• 卷积编码器(Convolution)：使用 1D 卷积学习运动的低维 latent embedding , 输出为 \(L \in R^{M \times N}\), M 是潜在特征(latent embedding)的维度(通道数)，也是卷积核的个数 \(L = enc(X), \quad L \in R^{M \times N}\) 在图中可以看到，经过卷积编码后曲线变稀疏了，原始曲线编码为潜在曲线 这里有一个问题，为什么要用低维的latent embedding，而不是升维，如果要做聚类分析的话

• FFT周期化：对经过卷积编码器的编码 \(L = (l_1, l_2, ... l_M)\) 中每个通道 \(l_t \in \mathcal{R}^N\), 有 \(\phi_t, f_t, a_t, b_t = p(l_t)\) 其中， p 表示使用 FFT 的参数化过程，每个\(\phi_t\)由一个单独训练的对应的全连接层(FC)得到, 这个参数表示不同的潜在曲线之间的时序关系.

• 重建参数化潜在曲线Latent：根据得到的参数 \(频率 f, 幅度 a, 偏移 b, 相位 \phi\) 以及时间窗口 T (与帧数H相关)，重建 Latent 曲线 \(\hat{L} \in R^{M \times N} \\ \hat{l_t} = \hat{p}(\phi_t, f_t, a_t, b_t) = a_t \cdot sin(2 \pi(f_t T+\phi_t)) + b_t\)

• 反卷积编码器：通过 1D 反卷积编码器将 latent embedding 编码为与输入相同维度的运动曲线 \(Y = dec(\hat{L}), Y \in R^{d \times N}\)

• 损失函数：根据原始运动曲线(输入)与预测运动曲线的 MSE 损失训练网络 \(Loss = MSE(X, Y)\)

对于网络的理解：

首先明确一些基本概念：

• 运动剪辑(motion clip)：一个运动的完整过程
• 运动窗口(motion window)：一个运动过程中的局部连续帧集合
• 运动帧(frame)：运动过程中某一个时刻运动状态的截取

输出是根据输入时间窗口重建的，这与输入的时间窗口是不同的，即输出 \(Y\) 实际是插值数据，输出的时间窗口是输入时间窗口对应的中心时间窗口(关于中心时间窗口可以参考原论文)

这种网络结构促使网络学习不同运动剪辑(motion clip)中的运动姿势对齐(关键帧的对齐)，并以单向的方式(仅依赖过去及现在的信息)为新运动帧(经过反卷积编码器重建的帧)分配变化的相位

同一个运动剪辑中，不同的时间窗口所重建的 Latent 变化的是相位的变化，其他属性如频率等均变化不大(可以在下一节中 Fig.3. 中看到频率，幅度，偏移基本是平的)； 即模型必须有效的学习到相位的变化(反应运动的进行)来定位“流形曲线”，而其他关于这种运动性质属性基本不变； 这一点在网络中最后落在模型必须有效学习一个旋转的2D向量(Atan2)来改变其需要重建的输入曲线的Latent的周期嵌入值

3. 相位流形

下面，研究如何根据Latent形成相位流形

使用训练后的网络，沿着运动曲线(motion clip dataset)移动，计算出其每一帧的Latent的周期参数；利用这些参数，我们形成一个维度为 \(2M\) 的流形 \(\mathcal{P}\)，即\(\mathcal{P} \in \mathbb{R}^{2M}, \quad M 为 Latent 的维度\) 这个流形由Latent的周期参数定义：\(\mathcal{P}_{2i-1}^{(t)} = A_i^{(t)} \cdot \sin{2\pi \cdot S_i^{(t)}}, \mathcal{P}_{2i}^{(t)} = A_i^{(t)} \cdot \cos{2\pi \cdot S_i^{(t)}}\)

这个流形中的特征很好的描述了输入运动X的帧的时序，并且有助于对齐同一类或不同类运动中的动作，也就是说，\(\mathcal{P}\) 中的特征可以充当神经运动合成或运动匹配的输入特征。

• 对于相位流形中属性的直观理解（不严谨）：每个通道并不一定对应一种显示的运动类型

参数	运动中的意义	作用
相位	运动的周期状态（如当前是迈左脚还是迈右脚）。	表示运动在周期中的位置，用于捕捉当前的运动阶段。
幅度	运动的强度或幅度（如步幅大小、挥手的力度）。	描述周期运动的强弱，区分运动类型和风格。
周期频率	运动模式的周期性频率（如步态频率，挥手快慢）。	表示周期性运动的速率(与整体速度不同，是这个运动模式的周期速度)
偏移	运动的基准位置或中心值	决定运动的整体位置，影响运动的静态特性

这些参数共同作用，用于建模和分解复杂运动。例如：

• 对于跑步，相位描述当前的步伐阶段，幅度表示步幅大小，频率反映跑步的快慢，偏移对齐不同人的跑步起始状态。
• 对于挥手，相位描述手在挥动周期中的位置，幅度描述挥动的力度，频率反映挥动的速度。

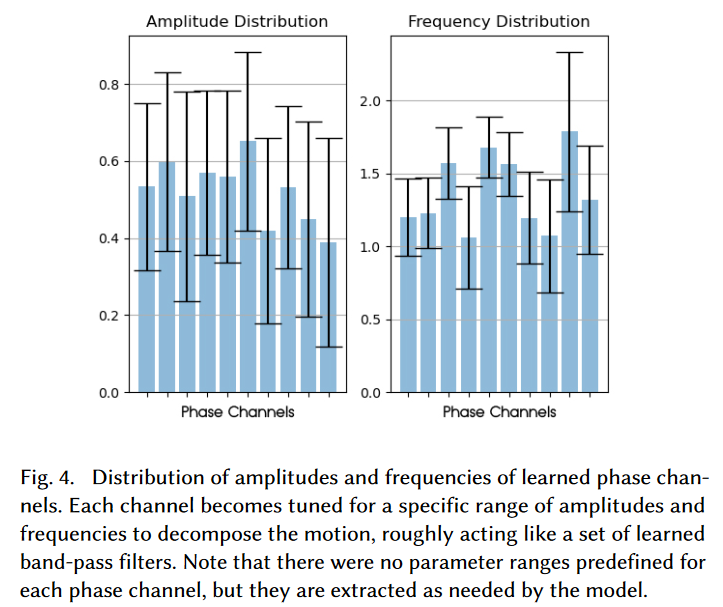
Fig.4. 展示了10个Latent通道对应的幅度和频率的分布，每个通道针对不同的频率学习特征，这些特征对应不同的运动速度(也可以理解为频率)；每个通道表现出来像一个带通滤波器。 纵轴上的条形代表均值的大小，黑色的范围代表变化范围

Fig.3. 整个图表示的是同一个运动窗口(motion window)中不同通道(Latent维度)的属性 从纵排列看，是Latent特征或通道；横排列是关于该通道对应的各个属性，第一个是由 \(A, F, B, \phi\) 构建的对应的相位流形维度上的值 \(\mathcal{P}_{2i-1}^{(t)} = A_i^{(t)} \cdot \sin{2\pi \cdot S_i^{(t)}}, \mathcal{P}_{2i}^{(t)} = A_i^{(t)} \cdot \cos{2\pi \cdot S_i^{(t)}}\) , 暂且认为这种波形可以表示相位流形。

每个子图，横坐标代表时间(时间帧变化)，纵坐标代表对应的属性值。

现在有了相位流形与周期特征的对应关系，以及一个时间窗口内，不同通道周期特征随时间的变化；那么，回到我们关注的问题：相位流形或者说周期特征是如何反应运动的

看一个例子

这张图中，每一行是一个相位通道(latent)，横坐标代表时间，纵坐标是该行对应的相位通道的值，代表一种独立的周期性运动模式；颜色的亮度表示每个时间点的相位值，透明度表示该相位的幅度值 这些周期性纹理反应了该motion clip的周期性运动模式。每一种周期性运动被分解到不同的相位通道中，每一行代表一种独立的周期性运动模式。在某些时间段内，某些相位通道表现出较高的周期振幅（较亮的区域），说明这一时间段的运动与该通道的周期性变化密切相关。

4. 网络训练

1. 输入，使用 3D 关节速度轨迹作为网络的输入，并减去基于窗口的均值以使运动曲线居中，但不应用任何标准偏差缩放以保持相对差异。输入数据以 60 Hz 帧速率(数据集的采样帧率为60Hz)覆盖中心帧周围的过去和未来各 60 帧（1 秒）。 这构造了一个输入向量 \(X \in \mathbb{R}^{3 \cdot d \times N}\) ，其中 d 是关节特征的数量，N = 60+60+1 = 121 (frame)是时间样本。3 代表 3D 坐标

2. 编码器 g，使用两个卷积层，产生映射 \(( 3 d × N ) → ( d × N ) → ( M × N )\) 每个卷积后面都有批量归一化和 tanh 激活函数，观察到批量归一化显著有助于稳定此任务的训练，并有助于防止潜在空间分布衰减或模型在训练时间过长时过度拟合。在计算其符号角之前，进一步对预测的相移矢量应用批量归一化

3. 解码器 h 再次涉及两个反卷积层，但仅在第一次反卷积之后应用批量归一化和 tanh 激活

4. 数据集：使用动作捕捉数据集，60Hz帧率，每个数据集用于训练不同的周期自编码器和运动生成器，这也导致在特定数据集上训练的模型只能处理对应的动作类型，对其他动作类型和过渡上泛化能力欠缺

5. latent个数的选择，一般 5 ~ 10 即足够，对于周期性较明显的运动例如走路，5 个 latent 即可，对于复杂的非单一周期性的运动 latent 数量更多

5. 相位流形可视化

对每个数据集进行latent计算后，将得到的潜在特征主成分投影到 2D 平面上（Fig.6. 底部），为了进行比较，通过用全连接层替换相位层来计算嵌入，并在计算它们的 PC 后类似地将它们投影到 2D 平面（见Fig.6. 中间）。最后还绘制了原始关节速度的 PC（见Fig.6. 顶部）。同一颜色即同一运动剪辑(motion clip)即同一运动过程 可以看出，相位流形对于运动模式的聚类效果很好，具有类似于极坐标的一致结构。周期代表各个运动的主要周期，其中时间由围绕中心的角度表示，幅度作为运动的速度。此外，样本在不同幅度或频率的周期之间平滑过渡，这表明运动之间的过渡点。

具体实验结果较繁杂，不再赘述

6. 不足与待改进

相位流形虽然可以很好地表示运动模式，但在多个可能动作之间的选择上，它无法独自解决歧义问题。需要用户提供明确的指令或通过概率分布进行随机选择。通过这种方式，可以有效生成符合期望的具体运动技能，而不仅仅是依赖流形的聚类结果。

FLD 的改进

在 PAE 中，得到的潜在特征的频率、振幅、偏移基本不随时间变化，据此，可以提出傅里叶潜式动力学，认为频率、振幅、偏移是时间不变量，根据 t 时刻的潜在相位，可以预测 t+i 时刻的潜在相位

对于一个时间窗口，帧数为 H \(\mathbf{S}_t = (s_{t-H+1},...,s_t), \quad S \in \mathcal{R}^{d \times H}\) 可以得到其潜在特征 \(\mathbf{Z}_t = (z_{t-H+1}, ..., z_t), \quad Z \in \mathcal{R}^{c \times H}\) 其中 \(z_i = \textbf{enc}(s_i), \quad \phi_i, f_i, a_i, b_i = p(z_i), \quad i = 1,2,...,c\) p 表示对卷积处理后某个通道的傅里叶参数化过程

基于傅里叶潜式动力学的时间不变量假设，可以根据 t 时刻的潜在特征预测 t+i 时刻的潜在特征 \(\hat{z}_{t+i}' = \hat{p} (\phi_t + i f_t \Delta t, f_t, a_t, b_t)\) 对应的原始空间中的状态为 \(\hat{s}_{t+i}' = \textbf{dec}(\hat{z}_{t+i}') \\ \hat{\mathbf{S}}_{t+i}' = (\hat{s}_{t-H+1+i}', ... ,\hat{s}_t')\) 其中 \(\Delta t\) 是一个时间步长度 损失函数为 \(L_{FLD}^N = \sum_{i=0}^{N} \alpha^iL_i, \quad L_i = MSE(\hat{S}_{t+i}',S_{t+i})\) \(L_{t+i}\) 表示从 t 时刻向后移动 i 个时间步的时间窗口重建预测向量与输入实际向量的误差

使用 \(\alpha_i\) 作为时间衰减系数，N 为传播视界，是两个关键参数

这个损失函数的意义为：构建潜在特征时，要综合考虑从当前时间窗口到后面一段的时间窗口(这隐含着认为运动模式在一段时间内表现的潜在特征应当是稳定不变的，更远的运动的影响应当衰减更多)。N 代表了需要考虑的时间范围，越大即认为这个运动模式保持不变的时间越长，并且更考虑整体；衰减系数对应着这个影响的程度；综合N和a平衡局部和整体。